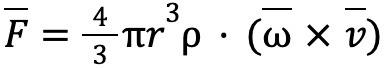Bernoulli's theory and Magnus Effect-Airplane and Panenka

A brief introduction to Bernoulli's aerodynamics and Magnus effect

In the World Cup 2018, Mr. Cristiano Ronaldo did a hat trick by sending a ball right over the defenders' heads. The ball descends straight down very quickly, right after passing the defenders. What a great skill demonstration. Our whole family cheers after seeing this, even though I am not Portuguese. Have you ever wondered how the "elevator kick" is performed? 

You must have seen Tiger Woods' incredible recovery shot if you are a golf fan. He had an incredible open stand and sliced the ball hard to make it go around the trees and land perfectly on the green. Why would the ball curve in such an incredible fashion?

All these phenomena and questions lead to our central topic today--- Bernoulli's theory and the Magnus Effect. Let's have a look at what they are. 

The German physicist Heinrich Gustav Magnus described the effect in 1852. However, in 1672, Isaac Newton described it and correctly inferred the cause after observing tennis players in his Cambridge college. In 1742, Benjamin Robins, a British mathematician, ballistics researcher, and military engineer, explained deviations in the trajectories of musket balls in terms of the Magnus effect.

The Magnus effect describes the behaviour of an object typically moving through a fluid. For example, a ball goes through the air, or a spinning thing breaks through the water. Essentially, the original path of the movement of the spinning ball would be deflected from the track when the ball is not spinning. 

Before getting to know the Magnus effect, let's first look at some basic conceptual ideas and theorems. In aerodynamics, the concepts of lift are closely related to Bernoulli's theory. Daniel Bernoulli is a Swiss mathematician and physicist who proposed the Bernoulli principle in 1738. Intuitively, the principle describes that the air pressure is lower when the air flows faster, and air pressure is higher when the air flows slowly. However, this statement is comparative, meaning that the determination of high and low pressure is relative. Let me give you a real-life example--- 

We all know that the design of aeroplane wings allows the planes to ascend into the air. But how does that really work? 

In the aeroplane wing scenario, the airflow is divided into two paths. One goes above the wing, and one goes under. And as demonstrated in the figure, the top of the wing is curved while the bottom is usually flat. The difference in the curvature makes air above and under the wing travel different distances: the air has a greater distance to cover above the wing. However, since the amount of time it takes to cover the distances is the same, we can conclude that air flows faster above the wing. Then, according to Bernoulli, since the air pressure under the wing is higher, the wing will be pushed up, which is why aeroplanes ascend. 

The derivation of the Bernoulli principle can be intuitively understood as an application of energy conservation. So, in a steady flow, the sum of all forms of energy will be the same for all the points in the streamflow: the point at the bottom-left of the flow will be the same as the point at the top-right. In this case, the kinetic, potential, and internal energy would be the same for these points. When part of the air flows faster in streamline, its kinetic energy is greater than the rest. Then, its internal and potential energy(including the static pressure) would decrease. That's where the "faster flow, smaller pressure" comes from. 

The Magnus effect would be a case involving Bernoulli's theory. Let's consider a spinning ball moving to the left. The airflow, as indicated, goes to the right. At the same time, the ball is also spinning clockwise, as shown by the arrows. In this case, the top of the ball, labelled by the blue arrow, travels in the same direction as the airflow (to the right). On the other hand, the bottom of the ball, labelled by the red arrow, travels against the airflow (one goes left, and one goes left). Due to the ball's spin, the air would flow faster on the top and slower on the bottom. Relating this to the Bernoulli theory we talked about, that "greater flow, smaller pressure," the pressure on the bottom would, in turn, be greater than the pressure on the top. Because of this difference in air pressure, the ball would be forced against gravity and inclines to go upward. In this graph, I used a soccer ball as an indication. You can think of this motion as a Panenka kick in soccer. 

By attacking the bottom of the ball only and creating backspin on the ball, the player makes the soccer ball undergo the Magnus effect. As illustrated in the previous paragraph, the ball tends to go upward, resulting in a relatively high and smooth trajectory. 

If you would like to explore the Magnus effect further, you can look at this expression of it. The force causing the ball to rise can be expressed as: 

"F" is the force. "S" is a coefficient related to the surface's viscosity resistance. "w" is the angular velocity and "v" is the velocity. The direction of cross multiplication of the two vectors follows the right-hand rule. To summarise, we see the resultant force is related to the viscosity resistance, how fast the ball is spinning and how quickly the ball is travelling. To expand it a little bit more, for a smooth spherical object, the force can be written as---

(4/3pir^3 would just be the volume of the ball, and p represents fluid density) In this case, the size of the ball and the material the ball travels in aslo matters. 

It's interesting how the theories of aerodynamics, in particular, Bernoulli's theory and Magnus's effect, can have so much connection to our everyday life. From the design of aeroplane wings to the fascinating techniques in sports. It's indeed essential to consider the theoretical behind our daily experiences. In this way, the knowledge of science can improve the efficiency of your execution and make you a more thoughtful human being.